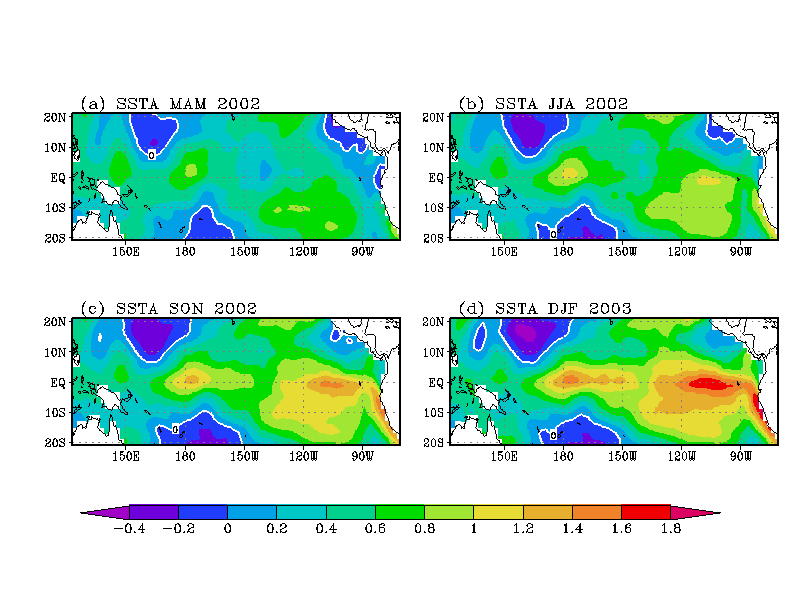
The nonlinear canonical correlation analysis (NLCCA), developed by Hsieh (2000) using a neural network (NN) approach, has been applied to study the nonlinear relation between the tropical Pacific sea level pressure (SLP) and sea surface temperature (SST) fields (Hsieh, 2001), as well as between the wind stress and SST fields (Wu and Hsieh, 2002). Here the NLCCA model is used for the seasonal forecasts of the tropical Pacific SST from the SLP.
The monthly tropical Pacific SLP data (COADS, Woodruff et al. 1987) and the monthly tropical Pacific SST data (Smith et al. 1996) had their seasonal cycles and linear trends removed, and a 3-month running mean applied. As we are still experimenting with the NLCCA approach, the setup of the present NLCCA model differs from that in an earlier issue (Wu and Hsieh, 2001). Predictands are the 6 leading principal components (PCs) of the SST anomalies (SSTA). Predictors are the 10 leading PCs from the singular spectrum analysis (i.e. extended EOF) of the SLP anomalies with a 9-month lag window. The predictors and predictands are the inputs to the NLCCA model. For cross-validation, 5 different models were built. The first was built without the data from 1950-1959, which was to be used as independent validation (or testing) data. Similarly, each of the other models had a different decade of data left out for independent validation.
Due to local minima problems in finding nonlinear modes, only the leading NLCCA mode was used. From the residual data, the linear CCA was used to extract additional modes. Hence the NLCCA forecasts actually use the leading NLCCA mode plus 4 CCA modes. The CCA model uses 5 CCA modes. Using more modes lead to decreasing forecast skills. Table 1 shows the forecasts skills from the nonlinear approach and from the linear approach. Note that for the Nino3.4 and Nino4 regions, at lead times 9 months or longer, the nonlinear approach was marginally worse than the linear approach, due to local minima problems during the nonlinear optimization.
Correlation RMSE
----------------------------------------------------------------------------
lead Nino1+2 Nino3 Nino3.4 Nino4 Nino1+2 Nino3 Nino3.4 Nino4
----------------------------------------------------------------------------
0 0.848 0.928 0.935 0.884 0.57 0.31 0.28 0.27
3 0.701 0.828 0.859 0.823 0.78 0.47 0.41 0.34
CCA 6 0.464 0.657 0.722 0.725 1.04 0.67 0.58 0.42
9 0.423 0.537 0.598 0.627 1.11 0.77 0.68 0.49
12 0.394 0.483 0.507 0.528 1.19 0.84 0.78 0.56
15 0.280 0.454 0.488 0.487 1.26 0.85 0.77 0.57
----------------------------------------------------------------------------
0 0.833 0.923 0.935 0.903 0.60 0.32 0.28 0.25
3 0.727 0.829 0.864 0.845 0.75 0.47 0.40 0.31
NLCCA 6 0.522 0.668 0.735 0.735 0.97 0.65 0.56 0.41
9 0.431 0.550 0.597 0.615 1.05 0.74 0.68 0.50
12 0.439 0.517 0.506 0.509 1.06 0.77 0.76 0.56
15 0.302 0.466 0.470 0.467 1.14 0.80 0.77 0.58
----------------------------------------------------------------------------